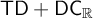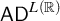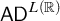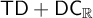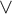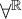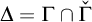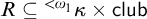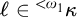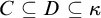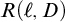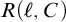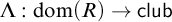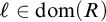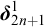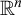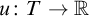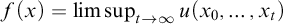Refine search
Actions for selected content:
61 results
Investigation into phenomena surrounding universally Baire sets
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 15 December 2025, pp. 695-696
- Print publication:
- December 2025
-
- Article
-
- You have access
- Export citation
Chapter 7 - An Apparatus for Cognition
- from Part II - A Kantian Account of Thought Experiment
-
- Book:
- Kierkegaard and the Structure of Imagination
- Published online:
- 26 September 2025
- Print publication:
- 16 October 2025, pp 107-118
-
- Chapter
- Export citation
SIZE OF PIECES IN DECOMPOSITIONS INTO THE FIRST UNCOUNTABLE CARDINAL MANY PIECES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON WINNING STRATEGIES FOR
 $F_\sigma $ GAMES
$F_\sigma $ GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-15
-
- Article
- Export citation
CARNAP’S (CATEGORICITY) PROBLEM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 July 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Practical Reason in Peril
- from Part II - Key Rhetorical Concepts Animating Contemporary American Law
-
-
- Book:
- Rhetorical Traditions and Contemporary Law
- Published online:
- 02 May 2025
- Print publication:
- 22 May 2025, pp 70-94
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Effect of a cost channel on monetary policy transmission in a behavioral new Keynesian model
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 19 May 2025, e104
-
- Article
- Export citation
Chapter 6 - Cultural Stereotype
-
- Book:
- Cultural Stereotype and Its Hazards
- Published online:
- 21 November 2024
- Print publication:
- 28 November 2024, pp 180-217
-
- Chapter
- Export citation
Chapter 1 - Introduction
-
- Book:
- The Largest Suslin Axiom
- Published online:
- 07 June 2024
- Print publication:
- 27 June 2024, pp 1-8
-
- Chapter
- Export citation

The Largest Suslin Axiom
-
- Published online:
- 07 June 2024
- Print publication:
- 27 June 2024
New evidence on US monetary policy activism and the Taylor rule
-
- Journal:
- Macroeconomic Dynamics / Volume 28 / Issue 8 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1809-1832
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Answering Kripke’s Skeptic
-
-
- Book:
- Kripke's <i>Wittgenstein on Rules and Private Language</i> at 40
- Published online:
- 22 February 2024
- Print publication:
- 08 February 2024, pp 55-68
-
- Chapter
- Export citation
NOTE ON
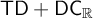 $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 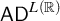 $\mathsf {AD}^{L(\mathbb {R})}$
$\mathsf {AD}^{L(\mathbb {R})}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 211-217
- Print publication:
- March 2024
-
- Article
- Export citation
Remarks on labelling and determinacy
-
- Journal:
- Canadian Journal of Linguistics/Revue canadienne de linguistique / Volume 68 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 August 2023, pp. 307-316
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - The Content of Coherence
-
- Book:
- Manifestations of Coherence and Investor-State Arbitration
- Published online:
- 13 December 2022
- Print publication:
- 19 January 2023, pp 11-35
-
- Chapter
- Export citation
COUNTABLE LENGTH EVERYWHERE CLUB UNIFORMIZATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1556-1572
- Print publication:
- December 2023
-
- Article
- Export citation
DETERMINACY OF SCHMIDT’S GAME AND OTHER INTERSECTION GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1-21
- Print publication:
- March 2023
-
- Article
- Export citation
GAMES CHARACTERIZING LIMSUP FUNCTIONS AND BAIRE CLASS 1 FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1459-1473
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Conclusion: Competing Normative Cultures of War
- from Part III - Managing Uncertainty: Reconciling Legal and Extra-legal Reasoning
-
- Book:
- Law, War and the Penumbra of Uncertainty
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 310-330
-
- Chapter
- Export citation
CONSTRUCTING WADGE CLASSES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 207-257
- Print publication:
- June 2022
-
- Article
- Export citation