Refine search
Actions for selected content:
23 results
On contemporary mortality models for actuarial use II: principles
-
- Journal:
- British Actuarial Journal / Volume 30 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kalikow decomposition for counting processes with stochastic intensity and application to simulation algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1469-1500
- Print publication:
- December 2023
-
- Article
- Export citation
1 - Counting Processes
- from Part I - Point Processes
-
- Book:
- Point Processes and Jump Diffusions
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 3-7
-
- Chapter
- Export citation
An elementary derivation of moments of Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 102-137
- Print publication:
- March 2020
-
- Article
- Export citation
DIFFUSION LIMITS FOR A MARKOV MODULATED BINOMIAL COUNTING PROCESS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 235-257
-
- Article
- Export citation
The DFR Property for Counting Processes Stopped at an Independent Random Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 574-585
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Simple derivations of properties of counting processes associated with Markov renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1031-1043
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Statistical properties of a system reliability estimator using the Littlewood software reliability model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 766-778
- Print publication:
- September 2003
-
- Article
- Export citation
Super-Efficient Prediction Based on High-Quality Marker Information
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 30 / Issue 2 / November 2000
- Published online by Cambridge University Press:
- 29 August 2014, pp. 295-303
- Print publication:
- November 2000
-
- Article
-
- You have access
- Export citation
The asymptotic final size distribution of multitype chain-binomial epidemic processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 220-234
- Print publication:
- March 1999
-
- Article
- Export citation
The evolution and measurement of a population of pairs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1048-1062
- Print publication:
- December 1995
-
- Article
- Export citation
A multitype decomposable age-dependent branching process and its applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 591-608
- Print publication:
- September 1995
-
- Article
- Export citation
A functional central limit theorem for the jump counts of Markov processes with an application to Jackson networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 476-509
- Print publication:
- June 1995
-
- Article
- Export citation
Logarithmic asymptotics for steady-state tail probabilities in a single-server queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-156
- Print publication:
- 1994
-
- Article
- Export citation
Partially observable semi-Markov reward processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 548-560
- Print publication:
- September 1993
-
- Article
- Export citation
A general risk process and its properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-81
- Print publication:
- March 1992
-
- Article
- Export citation
A note on random intensities and conditional survival functions
-
- Journal:
- Journal of Applied Probability / Volume 25 / Issue 3 / September 1988
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-635
- Print publication:
- September 1988
-
- Article
- Export citation
The distributional structure of finite moving-average processes
-
- Journal:
- Journal of Applied Probability / Volume 25 / Issue 2 / June 1988
- Published online by Cambridge University Press:
- 14 July 2016, pp. 313-321
- Print publication:
- June 1988
-
- Article
- Export citation
The structure of elementary pure birth processes
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 3 / September 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 664-667
- Print publication:
- September 1982
-
- Article
- Export citation
Filtering counts of cars entering and leaving a parking place
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 1 / March 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 64-71
- Print publication:
- March 1982
-
- Article
- Export citation
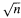 -consistently if a high quality marker is observed. In this paper we show that the hazard relevant for predicting remaining duration time, given the current status of a high quality marker, can be estimated
-consistently if a high quality marker is observed. In this paper we show that the hazard relevant for predicting remaining duration time, given the current status of a high quality marker, can be estimated 