Refine search
Actions for selected content:
20 results
The range of the Douglas–Rachford operator in infinite-dimensional Hilbert spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-18
-
- Article
- Export citation
1 - First Acquaintance with Convex Sets
- from Part I - Convex sets in Rn: From First Acquaintance to Linear Programming Duality
-
- Book:
- Essential Mathematics for Convex Optimization
- Published online:
- 22 October 2025
- Print publication:
- 26 June 2025, pp 3-27
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Polytopes and Graphs
- Published online:
- 14 March 2024
- Print publication:
- 21 March 2024, pp 1-43
-
- Chapter
- Export citation
2 - Preliminaries
-
- Book:
- Large-Scale System Analysis Under Uncertainty
- Published online:
- 17 January 2022
- Print publication:
- 17 February 2022, pp 16-53
-
- Chapter
- Export citation
3 - Graphical Linear Programming
-
- Book:
- Invitation to Linear Programming and Game Theory
- Published online:
- 11 March 2021
- Print publication:
- 11 March 2021, pp 102-147
-
- Chapter
- Export citation
Lineability, continuity, and antiderivatives in the non-Archimedean setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 638-650
- Print publication:
- September 2021
-
- Article
- Export citation
DUALITY FOR QUASIPOLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 95-117
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
SEPARATION OF CONVEX SETS IN EXTENDED NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 145-165
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Exact null internal controllability for the heat equation on unbounded convex domains∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, pp. 222-235
- Print publication:
- January 2014
-
- Article
- Export citation
Higher Connectedness Properties of Support Points and Functionals of Convex Sets
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1236-1254
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Length and surface area estimation under smoothness restrictions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 348-358
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
On the Hausdorff distance between a convex set and an interior random convex hull
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 295-316
- Print publication:
- June 1998
-
- Article
- Export citation
Rates of convergence for random approximations of convex sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 384-393
- Print publication:
- June 1996
-
- Article
- Export citation
Analysis of planar anisotropy by means of the Steiner compact
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 3 / September 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 490-502
- Print publication:
- September 1989
-
- Article
- Export citation
A geometric property of convex sets with applications to minimax type inequalities and fixed point theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-183
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
On Fixed Points of Asymptotically Regular Mappings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-346
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
Fixed points of certain involutions in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-177
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Some new integral geometric formulae, with stochastic applications
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 3 / September 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 592-606
- Print publication:
- September 1979
-
- Article
- Export citation
Direct derivations of certain surface integral formulae for the mean projections of a convex set
-
- Journal:
- Advances in Applied Probability / Volume 7 / Issue 4 / December 1975
- Published online by Cambridge University Press:
- 01 July 2016, pp. 818-829
- Print publication:
- December 1975
-
- Article
- Export citation
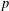
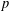
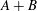
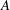
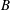
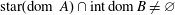
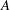
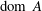
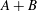


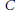
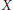
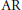
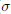
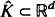 is studied. Basic inequalities are derived for the case of
is studied. Basic inequalities are derived for the case of 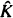 being a convex subset of
being a convex subset of 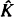 being the intersection of a random family of halfspaces containing
being the intersection of a random family of halfspaces containing 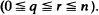 Stochastic applications in
Stochastic applications in 