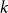Refine search
Actions for selected content:
4 results
Satisfiability thresholds for regular occupation problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 491-527
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
33 - Strong Data-Processing Inequality
- from Part VI - Statistical Applications
-
- Book:
- Information Theory
- Published online:
- 09 January 2025
- Print publication:
- 02 January 2025, pp 642-676
-
- Chapter
- Export citation
11 - Flow Measurement
- from Part II - Principles of Hydraulics
-
- Book:
- Irrigation Engineering
- Published online:
- 05 August 2022
- Print publication:
- 07 July 2022, pp 195-212
-
- Chapter
- Export citation
The Contraction Coefficient of a Free-Surface Flow Under Gravity Entering a Region Beneath a Semi-Infinite Plane
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 2 / Issue 4 / November 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 342-352
- Print publication:
- November 2012
-
- Article
- Export citation