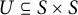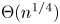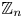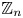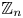Refine search
Actions for selected content:
63 results
8 - A Uniformitarian Lens on Creole Languages
-
-
- Book:
- Uniformitarianism in Language Speciation
- Published online:
- 10 December 2025
- Print publication:
- 18 December 2025, pp 310-336
-
- Chapter
- Export citation
When salience undermines representation: democratic dilemmas in security and counterterrorism policy
-
- Journal:
- Political Science Research and Methods , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Essays in Classical Number Theory
-
- Published online:
- 12 August 2025
- Print publication:
- 28 August 2025
SEMIGROUP CONGRUENCES AND SUBSEMIGROUPS OF THE DIRECT SQUARE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MONOTONIC COLLATZ SUBSEQUENCES WITH TERMS CONGRUENT MODULO A FIXED POWER OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 418-429
- Print publication:
- December 2025
-
- Article
- Export citation
16 - Trapped surfaces, event horizons, causality, and topology
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 168-179
-
- Chapter
- Export citation
11 - A Matter of Degree: All Languages are Mixed
- from Part III - The Development of Syntax
-
-
- Book:
- The Evolution, Acquisition and Development of Syntax
- Published online:
- 19 February 2025
- Print publication:
- 06 February 2025, pp 193-208
-
- Chapter
- Export citation
Orthogonal Rotations to Maximal Agreement for Two or More Matrices of Different Column Orders
-
- Journal:
- Psychometrika / Volume 49 / Issue 1 / March 1984
- Published online by Cambridge University Press:
- 01 January 2025, pp. 49-55
-
- Article
- Export citation
4 - Norm Research on Conflictive Norm Relations
- from Part I - Norm Strength, Collisions, and Conflicts
-
-
- Book:
- Contesting the World
- Published online:
- 01 November 2024
- Print publication:
- 06 June 2024, pp 64-82
-
- Chapter
- Export citation
Campaign communication and legislative leadership
-
- Journal:
- Political Science Research and Methods / Volume 13 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 04 April 2024, pp. 545-566
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Measuring Political Inequality
- from Part I - Government Responsiveness
-
-
- Book:
- Unequal Democracies
- Published online:
- 07 December 2023
- Print publication:
- 21 December 2023, pp 77-97
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 331-362
- Print publication:
- June 2024
-
- Article
- Export citation
Congruence in positive implicit followership theories, relational identification, and job performance: The moderating role of uncertainty avoidance
-
- Journal:
- Journal of Management & Organization / Volume 30 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1170-1189
-
- Article
- Export citation
16 - Religious Pluralism and Social Unions
- from Part IV - Pluralism, Democracy, and the Future of Justice as Fairness
-
-
- Book:
- Rawls’s <i>A Theory of Justice</i> at 50
- Published online:
- 20 July 2023
- Print publication:
- 10 August 2023, pp 277-295
-
- Chapter
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1180-1197
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Rich Have a Slight Edge: Evidence from Comparative Data on Income-Based Inequality in Policy Congruence
-
- Journal:
- British Journal of Political Science / Volume 54 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 514-525
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On minimal ideals in pseudo-finite semigroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 2007-2037
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
5 - Ideals
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 104-125
-
- Chapter
- Export citation
8 - Modules
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 171-188
-
- Chapter
- Export citation