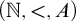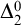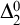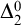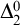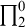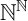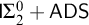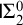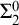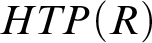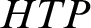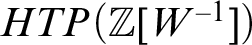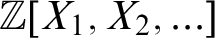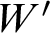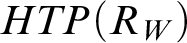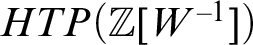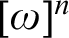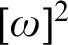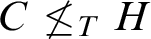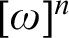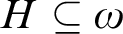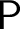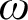Refine search
Actions for selected content:
26 results
THE COMPLEXITY OF ORDER-COMPUTABLE SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-24
-
- Article
- Export citation
16 - Open Problems
-
- Book:
- The Theory of Countable Borel Equivalence Relations
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 137-141
-
- Chapter
- Export citation
A
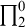 $ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
$ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTROENUMERABILITY, AUTOREDUCIBILITY, AND RANDOMNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 December 2023, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computability Theory on Polish Metric Spaces
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 664
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
Ordered Groups, Computability and Cantor-Bendixson Rank
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 664
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
(EXTRA)ORDINARY EQUIVALENCES WITH THE ASCENDING/DESCENDING SEQUENCE PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 December 2022, pp. 262-307
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Theoretical Computer Science for the Working Category Theorist
-
- Published online:
- 25 January 2022
- Print publication:
- 03 March 2022
-
- Element
- Export citation
THE DISCONTINUITY PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 January 2022, pp. 1191-1212
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE REVERSE MATHEMATICS OF THE THIN SET AND ERDŐS–MOSER THEOREMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 November 2021, pp. 313-346
- Print publication:
- March 2022
-
- Article
- Export citation
HTP-COMPLETE RINGS OF RATIONAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 252-272
- Print publication:
- March 2022
-
- Article
- Export citation
RAMSEY-LIKE THEOREMS AND MODULI OF COMPUTATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 27 October 2020, pp. 72-108
- Print publication:
- March 2022
-
- Article
- Export citation
RELATIONSHIPS BETWEEN COMPUTABILITY-THEORETIC PROPERTIES OF PROBLEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 47-71
- Print publication:
- March 2022
-
- Article
- Export citation
1 - Key developments in algorithmic randomness
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 1-39
-
- Chapter
- Export citation
6 - Aspects of Chaitin’s Omega
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 175-205
-
- Chapter
- Export citation
3 - Algorithmic randomness and constructive/computable measure theory
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 58-114
-
- Chapter
- Export citation
9 - Resource bounded randomness and its applications
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 301-348
-
- Chapter
- Export citation
RANDOMNESS NOTIONS AND REVERSE MATHEMATICS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 09 September 2019, pp. 271-299
- Print publication:
- March 2020
-
- Article
- Export citation
DEGREES OF CATEGORICITY ON A CONE VIA η-SYSTEMS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 325-346
- Print publication:
- March 2017
-
- Article
- Export citation
STRONG REDUCTIONS BETWEEN COMBINATORIAL PRINCIPLES
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1405-1431
- Print publication:
- December 2016
-
- Article
- Export citation