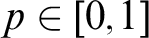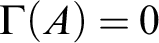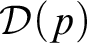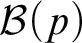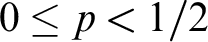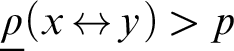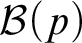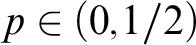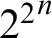Refine search
Actions for selected content:
30 results
A SHORT NOTE ON THE SIGNIFICANCE OF THE PENROSE-HALTING THEOREM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complexity of inversion of functions on the reals
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 27 October 2025, e26
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the isomorphism problem between multidimensional substitutive subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2054-2094
- Print publication:
- July 2025
-
- Article
- Export citation
20 - Computing in Soil Mechanics
-
- Book:
- A Primer on Theoretical Soil Mechanics
- Published online:
- 14 July 2022
- Print publication:
- 04 August 2022, pp 170-176
-
- Chapter
- Export citation
COMPLEXITY OF INDEX SETS OF DESCRIPTIVE SET-THEORETIC NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 894-911
- Print publication:
- September 2022
-
- Article
- Export citation
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
- Print publication:
- September 2022
-
- Article
- Export citation
4 - Artificial Economics versus Mathematics?
- from Part I - Artificial Economics and Mainstream Economics
-
- Book:
- Artificial Economics
- Published online:
- 28 October 2021
- Print publication:
- 04 November 2021, pp 60-70
-
- Chapter
- Export citation
DEGREES OF RANDOMIZED COMPUTABILITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 27-70
- Print publication:
- March 2022
-
- Article
- Export citation
8 - Analysis of Optimization Algorithms
- from Part II - Compressed Sensing, Optimization and Wavelets
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 166-187
-
- Chapter
- Export citation
21 - Stable and Accurate Neural Networks for Compressive Imaging
- from Part V - From Compressed Sensing to Deep Learning
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 501-520
-
- Chapter
- Export citation
Results on Martin’s Conjecture
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 219-220
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
3 - Computability: The Primary Example
-
- Book:
- Gödel, Tarski and the Lure of Natural Language
- Published online:
- 03 December 2020
- Print publication:
- 17 December 2020, pp 39-60
-
- Chapter
- Export citation
MUCHNIK DEGREES AND CARDINAL CHARACTERISTICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 04 September 2020, pp. 471-498
- Print publication:
- June 2021
-
- Article
- Export citation
COMPUTABILITY IN UNCOUNTABLE BINARY TREES
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1049-1098
- Print publication:
- September 2019
-
- Article
- Export citation
PERMUTATIONS OF THE INTEGERS INDUCE ONLY THE TRIVIAL AUTOMORPHISM OF THE TURING DEGREES
-
- Journal:
- Bulletin of Symbolic Logic / Volume 24 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 07 August 2018, pp. 165-174
- Print publication:
- June 2018
-
- Article
- Export citation
A COMPUTABLE FUNCTOR FROM GRAPHS TO FIELDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 326-348
- Print publication:
- March 2018
-
- Article
- Export citation
TURING DEGREE SPECTRA OF DIFFERENTIALLY CLOSED FIELDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 1-25
- Print publication:
- March 2017
-
- Article
- Export citation
FINITARY REDUCIBILITY ON EQUIVALENCE RELATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1225-1254
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
COMPARING TWO VERSIONS OF THE REALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 12 August 2016, pp. 1115-1123
- Print publication:
- September 2016
-
- Article
- Export citation