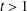Refine search
Actions for selected content:
14 results
Hyperspectral compressive wavefront sensing
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 March 2023, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse recovery properties of discrete random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 316-325
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Physical model-driven deep networks for through-the-wall radar imaging
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 15 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 82-89
-
- Article
- Export citation
5 - Mathematics and Compressed Sensing
- from Part II - Communications
-
- Book:
- Mathematics for Future Computing and Communications
- Published online:
- 03 December 2021
- Print publication:
- 16 December 2021, pp 138-152
-
- Chapter
- Export citation
5 - An Introduction to Conventional Compressed Sensing
- from Part II - Compressed Sensing, Optimization and Wavelets
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 105-128
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Compressive Imaging: Structure, Sampling, Learning
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021, pp 1-26
-
- Chapter
- Export citation
Compressive Imaging: Structure, Sampling, Learning
-
- Published online:
- 16 July 2021
- Print publication:
- 16 September 2021
6 - Uncertainty Relations and Sparse Signal Recovery
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 163-196
-
- Chapter
- Export citation
3 - Compressed Sensing via Compression Codes
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 72-103
-
- Chapter
- Export citation
14 - A Sparse Representation Approach for Anomaly Identification
- from Part IV - Signal Processing
-
-
- Book:
- Advanced Data Analytics for Power Systems
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 340-360
-
- Chapter
- Export citation
One-Bit Compressed Sensing by Greedy Algorithms
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 24 May 2016, pp. 169-184
- Print publication:
- May 2016
-
- Article
- Export citation
THE RESTRICTED ISOMETRY PROPERTY FOR SIGNAL RECOVERY WITH COHERENT TIGHT FRAMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 496-507
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Blind compressive sensing formulation incorporating metadata for recommender system design
-
- Journal:
- APSIPA Transactions on Signal and Information Processing / Volume 4 / 2015
- Published online by Cambridge University Press:
- 20 July 2015, e2
- Print publication:
- 2015
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Compressed Sensing Approach for Partial Differential Equations with Random Input Data
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 919-954
- Print publication:
- October 2012
-
- Article
- Export citation