Refine search
Actions for selected content:
1 results
Equivariant K-theory, groupoids and proper actions
-
- Journal:
- Journal of K-Theory / Volume 9 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 21 November 2011, pp. 475-501
- Print publication:
- June 2012
-
- Article
- Export citation
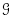 , this defines a periodic cohomology theory on the category of finite
, this defines a periodic cohomology theory on the category of finite 