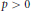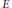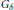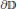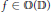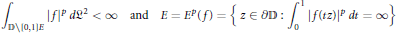Search

For 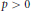$p\,>\,0$ and for a given set 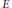$E$ of type 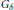${{G}_{\delta }}$ in the boundary of the unit disc 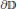$\partial \mathbb{D}$ we construct a holomorphic function 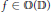$f\,\in \,\mathbb{O}\left( \mathbb{D} \right)$ such that

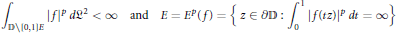$${{\int_{\mathbb{D}\backslash \left[ 0,\,1 \right]E}{\left| f \right|}}^{p}}\,d{{\mathfrak{L}}^{2}}\,<\,\infty \,\text{and}\,E\,=\,{{E}^{p}}\left( f \right)\,=\,\{\,z\,\in \,\partial \mathbb{D}\,:\,\int _{0}^{1}\,{{\left| f\left( tz \right) \right|}^{p}}\,dt\,=\,\infty \}.$$

In particular if a set 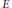$E$ has a measure equal to zero, then a function 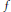$f$ is constructed as integrable with power 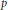$p$ on the unit disc 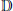$\mathbb{D}$ .

Assume that $\Omega$ is a Hartogs domain in ${{\mathbb{C}}^{1+n}}$ , defined as $\Omega =\left\{ \left( z,w \right)\,\in \,{{\mathbb{C}}^{1+n}}\,:\left| z \right|\,<\,\mu \left( w \right),w\,\in H \right\}$ , where $H$ is an open set in ${{\mathbb{C}}^{n}}$ and $\mu$ is a continuous function with positive values in $H$ such that –ln $\mu$ is a strongly plurisubharmonic function in $H$ . Let ${{\Omega }_{w}}=\Omega \cap \left( \mathbb{C}\times \left\{ w \right\} \right)$ . For a given set $E$ contained in $H$ of the type ${{G}_{\delta }}$ we construct a holomorphic function $f\in \mathbb{O}\left( \Omega\right)$ such that

$$E=\left\{ w\in {{\mathbb{C}}^{n}}:\int\limits_{{{\Omega }_{w}}}{{{\left| f\left( \cdot ,w \right) \right|}^{2}}d{{\mathfrak{L}}^{2}}=\infty } \right\}.$$

Search Results

Refine search

Refine search

Actions for selected content:

2 results

p-Radial Exceptional Sets and Conformal Mappings

Exceptional Sets in Hartogs Domains

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

p-Radial Exceptional Sets and Conformal Mappings

Exceptional Sets in Hartogs Domains