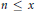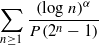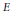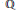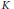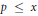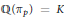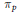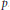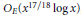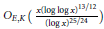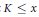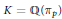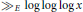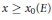We give an upper bound for the number of elliptic Carmichael numbers $n\,\le \,x$ that were recently introduced by J. H. Silverman in the case of an elliptic curve without complex multiplication (non $\text{CM}$ ). We also discuss several possible further improvements.

Let P(k) be the largest prime factor of the positive integer k. In this paper, we prove that the series is convergent for each constant α<1/2, which gives a more precise form of a result of C. L. Stewart [‘On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers’, Proc. London Math. Soc. 35(3) (1977), 425–447].

Let 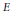$E$ be an elliptic curve defined over 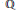$\mathbb{Q}$ and without complex multiplication. Let 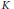$K$ be a fixed imaginary quadratic field. We find nontrivial upper bounds for the number of ordinary primes 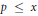$p\,\le \,x$ for which 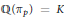$\mathbb{Q}\left( {{\pi }_{p}} \right)\,=\,K$ , where 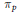${{\pi }_{p}}$ denotes the Frobenius endomorphism of 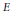$E$ at 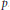$p$ . More precisely, under a generalized Riemann hypothesis we show that this number is 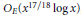${{O}_{E}}\left( {{x}^{17/18}}\,\log x \right)$ , and unconditionally we show that this number is 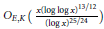${{O}_{E,K}}\left( \frac{x{{\left( \log \,\log x \right)}^{13/12}}}{{{\left( \log x \right)}^{25/24}}} \right)$ We also prove that the number of imaginary quadratic fields 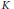$K$ , with − disc 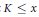$K\,\le \,x$ and of the form 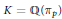$K\,=\,\mathbb{Q}({{\pi }_{p}})$ , is 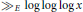${{\gg }_{E}}\,\log \,\log \,\log \,x$ for 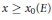$x\,\ge \,{{x}_{0}}\left( E \right)$ . These results represent progress towards a 1976 Lang–Trotter conjecture.