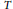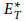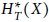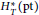Refine search
Actions for selected content:
11 results
A flag version of Beilinson–Drinfeld Grassmannian for surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - An Introduction to Affine Lie Algebras and the Associated Groups
-
- Book:
- Conformal Blocks, Generalized Theta Functions and the Verlinde Formula
- Published online:
- 19 November 2021
- Print publication:
- 25 November 2021, pp 1-67
-
- Chapter
- Export citation
GEOMETRY OF KOTTWITZ–VIEHMANN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1-65
- Print publication:
- January 2022
-
- Article
- Export citation
Corrigendum: Connected components of affine Deligne–Lusztig varieties in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 218-222
- Print publication:
- January 2017
-
- Article
-
- You have access
- HTML
- Export citation
The affine Grassmannian and the Springer resolution in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 28 November 2016, pp. 2627-2677
- Print publication:
- December 2016
-
- Article
- Export citation
Generalized Equivariant Cohomology and Stratifications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-496
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
Connected components of affine Deligne–Lusztig varieties in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 05 May 2015, pp. 1697-1762
- Print publication:
- September 2015
-
- Article
- Export citation
K-theory Schubert calculus of the affine Grassmannian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 811-852
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Equivariant homology and K-theory of affine Grassmannians and Toda lattices
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 746-768
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation















 .
.