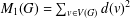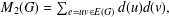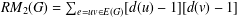Refine search
Actions for selected content:
4 results
ON SEVERAL PROPERTIES OF A CLASS OF PREFERENTIAL ATTACHMENT TREES—PLANE-ORIENTED RECURSIVE TREES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 4 / October 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 839-857
-
- Article
- Export citation
SOME RESULTS ON THE DIFFERENCE OF THE ZAGREB INDICES OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 177-186
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Phase Changes in the Topological Indices of Scale-Free Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 516-532
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
On the Zagreb Index of Random Recursive Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1189-1196
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation