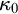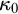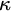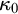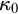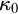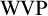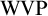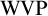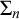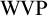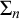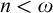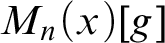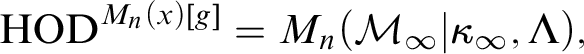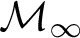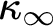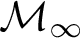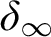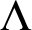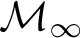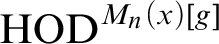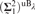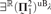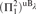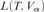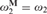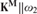Refine search
Actions for selected content:
7 results
WEAK INDESTRUCTIBILITY AND REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 980-1006
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRONG COMPACTNESS, SQUARE, GCH, AND WOODIN CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 August 2022, pp. 1180-1188
- Print publication:
- September 2024
-
- Article
- Export citation
THE WEAK VOPĚNKA PRINCIPLE FOR DEFINABLE CLASSES OF STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 June 2022, pp. 145-168
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
$\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 871-896
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIVERSALLY BAIRE SETS AND GENERIC ABSOLUTENESS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1229-1251
- Print publication:
- December 2017
-
- Article
- Export citation
DOWNWARD TRANSFERENCE OF MICE AND UNIVERSALITY OF LOCAL CORE MODELS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 385-419
- Print publication:
- June 2017
-
- Article
- Export citation
An equiconsistency for universal indestructibility
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 314-322
- Print publication:
- March 2010
-
- Article
- Export citation