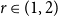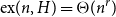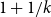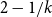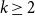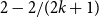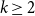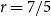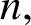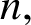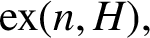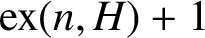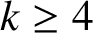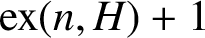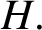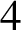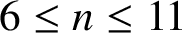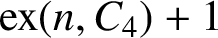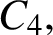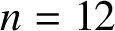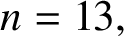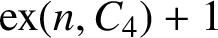The Erdős–Simonovits stability theorem is one of the most widely used theorems in extremal graph theory. We obtain an Erdős–Simonovits type stability theorem in multi-partite graphs. Different from the Erdős–Simonovits stability theorem, our stability theorem in multi-partite graphs says that if the number of edges of an $H$-free graph $G$ is close to the extremal graphs for $H$, then $G$ has a well-defined structure but may be far away from the extremal graphs for $H$. As applications, we strengthen a theorem of Bollobás, Erdős, and Straus and solve a conjecture in a stronger form posed by Han and Zhao concerning the maximum number of edges in multi-partite graphs which does not contain vertex-disjoint copies of a clique.

We consider the hypergraph Turán problem of determining $ex(n, S^d)$, the maximum number of facets in a $d$-dimensional simplicial complex on $n$ vertices that does not contain a simplicial $d$-sphere (a homeomorph of $S^d$) as a subcomplex. We show that if there is an affirmative answer to a question of Gromov about sphere enumeration in high dimensions, then $ex(n, S^d) \geq \Omega (n^{d + 1 - (d + 1)/(2^{d + 1} - 2)})$. Furthermore, this lower bound holds unconditionally for 2-LC (locally constructible) spheres, which includes all shellable spheres and therefore all polytopes. We also prove an upper bound on $ex(n, S^d)$ of $O(n^{d + 1 - 1/2^{d - 1}})$ using a simple induction argument. We conjecture that the upper bound can be improved to match the conditional lower bound.

A long-standing conjecture of Erdős and Simonovits asserts that for every rational number $r\in (1,2)$ there exists a bipartite graph H such that $\mathrm{ex}(n,H)=\Theta(n^r)$. So far this conjecture is known to be true only for rationals of form $1+1/k$ and $2-1/k$, for integers $k\geq 2$. In this paper, we add a new form of rationals for which the conjecture is true: $2-2/(2k+1)$, for $k\geq 2$. This in turn also gives an affirmative answer to a question of Pinchasi and Sharir on cube-like graphs. Recently, a version of Erdős and Simonovits$^{\prime}$s conjecture, where one replaces a single graph by a finite family, was confirmed by Bukh and Conlon. They proposed a construction of bipartite graphs which should satisfy Erdős and Simonovits$^{\prime}$s conjecture. Our result can also be viewed as a first step towards verifying Bukh and Conlon$^{\prime}$s conjecture. We also prove an upper bound on the Turán number of theta graphs in an asymmetric setting and employ this result to obtain another new rational exponent for Turán exponents: $r=7/5$.

We consider finite simple graphs. Given a graph H and a positive integer 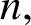$n,$ the Turán number of H for the order 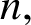$n,$ denoted 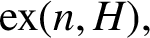$\mathrm {ex}(n,H),$ is the maximum size of a graph of order n not containing H as a subgraph. Erdős asked: ‘For which graphs H is it true that every graph on n vertices and 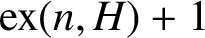$\mathrm {ex}(n,H)+1$ edges contains at least two H’s? Perhaps this is always true.’ We solve this problem in the negative by proving that for every integer 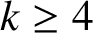$k\ge 4$ there exists a graph H of order k and at least two orders n such that there exists a graph of order n and size 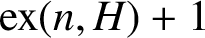$\mathrm {ex}(n,H)+1$ which contains exactly one copy of 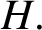$H.$ Denote by $C_4$ the 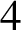$4$-cycle. We also prove that for every integer n with 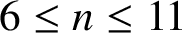$6\le n\le 11$ there exists a graph of order n and size 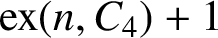$\mathrm {ex}(n,C_4)+1$ which contains exactly one copy of 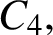$C_4,$ but, for 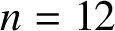$n=12$ or 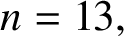$n=13,$ the minimum number of copies of $C_4$ in a graph of order n and size 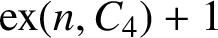$\mathrm {ex}(n,C_4)+1$ is two.