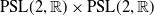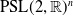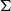Refine search
Actions for selected content:
5 results
Entropy stability and Milnor–Thurston invariants for Bowen–Series-like maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weyl chamber length compactification of the
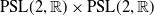 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Klein bottle group is not strongly verbally closed, though awfully close to being so
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 03 August 2020, pp. 491-497
- Print publication:
- June 2021
-
- Article
- Export citation
Simplicial complexity of surface groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 3153-3162
- Print publication:
- December 2020
-
- Article
- Export citation