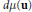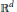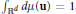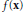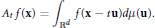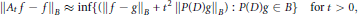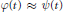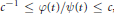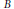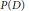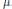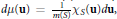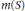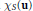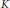For a positive finite measure 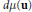$d\mu \left( \mathbf{u} \right)$ on 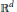${{\mathbb{R}}^{d}}$ normalized to satisfy 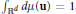$\int{_{{{\mathbb{R}}^{d}}}d\mu \left( \mathbf{u} \right)}=1$ , the dilated average of 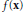$f\left( \mathbf{x} \right)$ is given by

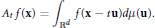$${{A}_{t}}\,f\left( \mathbf{x} \right)\,=\,\int{_{{{\mathbb{R}}^{d}}}\,f\left( \mathbf{x}\,-\,t\mathbf{u}\, \right)}d\mu \left( \mathbf{u} \right)$$

It will be shown that under some mild assumptions on 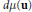$d\mu \left( \mathbf{u} \right)$ one has the equivalence

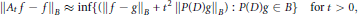$$||{A_t}f - f|{|_B} \approx \inf \left\{ {\left( {||f - g|{|_B} + {t^2}||P\left( D \right)g|{|_B}} \right):P\left( D \right)g \in B} \right\}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{for}}{\mkern 1mu} {\mkern 1mu} {\rm{t}}{\mkern 1mu} {\rm{> }}\,{\rm{0,}}$$

where 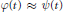$\varphi \left( t \right)\approx \psi \left( t \right)$ means 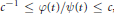${{c}^{-1}}\le \varphi \left( t \right)/\psi \left( t \right)\le c$ , 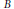$B$ is a Banach space of functions for which translations are continuous isometries and 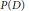$P\left( D \right)$ is an elliptic differential operator induced by 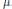$\mu $ . 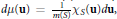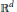Many applications are given, notable among which is the averaging operator with $d\mu \left( \mathbf{u} \right)\,=\,\frac{1}{m\left( S \right)}{{\chi }_{S}}\left( \mathbf{u} \right)d\mathbf{u},$ where $S$ is a bounded convex set in ${{\mathbb{R}}^{d}}$ with an interior point, 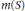$m\left( S \right)$ is the Lebesgue measure of $S$ , and 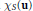${{\chi }_{S}}\left( \mathbf{u} \right)$ is the characteristic function of $S$ . The rate of approximation by averages on the boundary of a convex set under more restrictive conditions is also shown to be equivalent to an appropriate 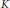$K$ -functional.