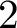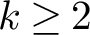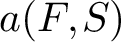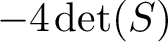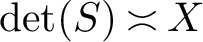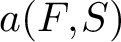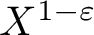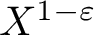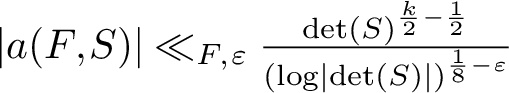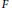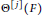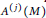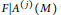Let F be a Siegel cusp form of degree 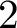$2$, even weight 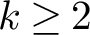$k \ge 2$, and odd square-free level N. We undertake a detailed study of the analytic properties of Fourier coefficients 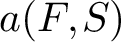$a(F,S)$ of F at fundamental matrices S (i.e., with 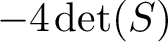$-4\det (S)$ equal to a fundamental discriminant). We prove that as S varies along the equivalence classes of fundamental matrices with 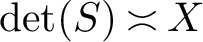$\det (S) \asymp X$, the sequence 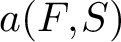$a(F,S)$ has at least 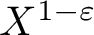$X^{1-\varepsilon }$ sign changes and takes at least 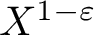$X^{1-\varepsilon }$ ‘large values’. Furthermore, assuming the generalized Riemann hypothesis as well as the refined Gan–Gross–Prasad conjecture, we prove the bound 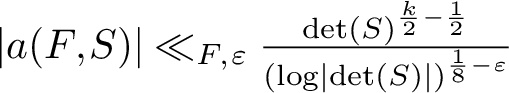$\lvert a(F,S)\rvert \ll _{F, \varepsilon } \frac {\det (S)^{\frac {k}2 - \frac {1}{2}}}{ \left (\log \lvert \det (S)\rvert \right )^{\frac 18 - \varepsilon }}$ for fundamental matrices S.

Let ${{\Theta }^{[j]}}$ be an analogue of the Ramanujan theta operator for Siegel modular forms. For a given prime $p$ , we give the weights of elements of mod $p$ kernel of ${{\Theta }^{[j]}}$ , where the mod $p$ kernel of ${{\Theta }^{[j]}}$ is the set of all Siegel modular forms $F$ such that ${{\Theta }^{[j]}}(F)$ is congruent to zero modulo $p$ . In order to construct examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ from any Siegel modular forms, we introduce new operators ${{A}^{(j)}}(M)$ and show the modularity of $F|{{A}^{\left( j \right)}}\left( M \right)$ when $F$ is a Siegel modular form. Finally, we give some examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ and the filtrations of some of them.