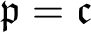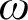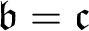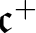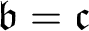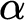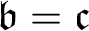Refine search
Actions for selected content:
1 results
THE RUDIN–KEISLER ORDERING OF P-POINTS UNDER 𝔟 = 𝔠
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1691-1705
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
M. E. Rudin (1971) proved, under CH, that for each P-point p there exists a P-point q strictly RK-greater than p. This result was proved under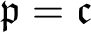
${\mathfrak {p}= \mathfrak {c}}$ by A. Blass (1973), who also showed that each RK-increasing 
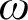$ \omega $-sequence of P-points is upper bounded by a P-point, and that there is an order embedding of the real line into the class of P-points with respect to the RK-ordering. In this paper, the results cited above are proved under the (weaker) assumption that 
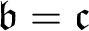$\mathfrak { b}=\mathfrak {c}$. A. Blass asked in 1973 which ordinals can be embedded in the set of P-points, and pointed out that such an ordinal cannot be greater than 
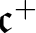$ \mathfrak {c}^{+}$. In this paper it is proved, under 
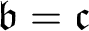$\mathfrak {b}=\mathfrak {c}$, that for each ordinal 
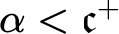$\alpha < \mathfrak {c}^{+}$, there is an order embedding of 
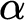$ \alpha $ into P-points. It is also proved, under 
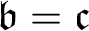$\mathfrak {b}=\mathfrak {c}$, that there is an embedding of the long line into P-points.
