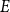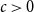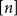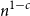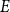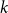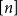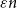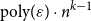Refine search
Actions for selected content:
2 results
Retirement tax shields: A cohort study of traditional and Roth accounts
-
- Journal:
- Journal of Pension Economics & Finance / Volume 24 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 392-413
-
- Article
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation