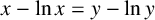Refine search
Actions for selected content:
1 results
ANALYTICAL APPROXIMATIONS OF LOTKA–VOLTERRA INTEGRALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation