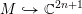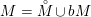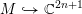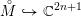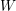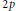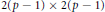Refine search
Actions for selected content:
10 results
2-Elongated plane partitions and powers of 7: the localization method applied to a genus 1 congruence family
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-43
-
- Article
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
Determinant of the Laplacian on Tori of Constant Positive Curvature with one Conical Point
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 341-347
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
NEW COMPLEX ANALYTIC METHODS IN THE THEORY OF MINIMAL SURFACES: A SURVEY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 23 August 2018, pp. 287-341
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Holomorphic Legendrian curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 29 June 2017, pp. 1945-1986
- Print publication:
- September 2017
-
- Article
- Export citation
Dihedral Groups of Order 2p of Automorphisms of Compact Riemann Surfaces of Genus p – 1
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-206
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
A NEW CHARACTERIZATION OF WIMAN SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 360-368
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
THE ROLE OF FUNNELS AND PUNCTURES IN THE GROMOV HYPERBOLICITY OF RIEMANN SURFACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 30 May 2006, pp. 399-425
-
- Article
-
- You have access
- Export citation
ALGEBRAIC CURVES, RIEMANN SURFACES AND KLEIN SURFACES WITH NO NON-TRIVIAL AUTOMORPHISMS OR SYMMETRIES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 05 February 2002, pp. 141-148
-
- Article
-
- You have access
- Export citation
Galois Covers of Moduli of Curves
-
- Journal:
- Compositio Mathematica / Volume 120 / Issue 2 / January 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 171-191
- Print publication:
- January 2000
-
- Article
-
- You have access
- Export citation