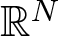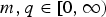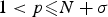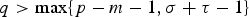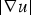Refine search
Actions for selected content:
8 results
Hardy-type inequalities for the drifting p-Laplace operator and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-existence theorems for quasilinear elliptic equations with weights
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-33
-
- Article
- Export citation
Symmetry via the moving plane method for a class of quasilinear elliptic problems involving the Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1858-1882
- Print publication:
- December 2023
-
- Article
- Export citation
Gradient estimates for nonlinear elliptic equations with a gradient-dependent nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1361-1376
- Print publication:
- June 2020
-
- Article
- Export citation
A priori bounds and multiplicity of positive solutions for p-Laplacian Neumann problems with sub-critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 73-102
- Print publication:
- February 2020
-
- Article
- Export citation
Existence of nodal solutions for quasilinear elliptic problems in ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 24 August 2015, pp. 937-957
- Print publication:
- October 2015
-
- Article
- Export citation
BOUNDED MULTIPLE SOLUTIONS FOR
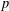 $p$-LAPLACIAN PROBLEMS WITH ARBITRARY PERTURBATIONS
$p$-LAPLACIAN PROBLEMS WITH ARBITRARY PERTURBATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 175-185
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Quasi-Optimal Convergence Rate of an AFEM for Quasi-Linear Problems of Monotone Type
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 5 / Issue 2 / May 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 131-156
- Print publication:
- May 2012
-
- Article
- Export citation