Refine search
Actions for selected content:
5 results
On (2,2)-decomposable genus 4 Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic Torelli theorem for Prym varieties of ramified coverings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 11 July 2012, pp. 1147-1170
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
The arithmetic of Prym varieties in genus 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 317-338
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
A necessary and sufficient condition for Riemann's singularity theorem to hold on a Prym theta divisor
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 447-458
- Print publication:
- March 2004
-
- Article
-
- You have access
- Export citation
The de Rham Bundle on a Compactification of Moduli Space of Abelian Varieties
-
- Journal:
- Compositio Mathematica / Volume 136 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 317-321
- Print publication:
- May 2003
-
- Article
-
- You have access
- Export citation















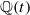 . By specialization, this also gives examples over
. By specialization, this also gives examples over 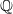 .
.