We consider stationary configurations of points in Euclidean space that are marked by positive random variables called scores. The scores are allowed to depend on the relative positions of other points and outside sources of randomness. Such models have been thoroughly studied in stochastic geometry, e.g. in the context of random tessellations or random geometric graphs. It turns out that in a neighborhood of a point with an extreme score it is possible to rescale positions and scores of nearby points to obtain a limiting point process, which we call the tail configuration. Under some assumptions on dependence between scores, this local limit determines the global asymptotics for extreme scores within increasing windows in $\mathbb{R}^d$. The main result establishes the convergence of rescaled positions and clusters of high scores to a Poisson cluster process, quantifying the idea of the Poisson clumping heuristic by Aldous (1989, in the point process setting). In contrast to the existing results, our framework allows for explicit calculation of essentially all extremal quantities related to the limiting behavior of extremes. We apply our results to models based on (marked) Poisson processes where the scores depend on the distance to the kth nearest neighbor and where scores are allowed to propagate through a random network of points depending on their locations.

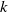Let $X_1,X_2, \ldots, X_n$ be a sequence of independent random points in $\mathbb{R}^d$ with common Lebesgue density f. Under some conditions on f, we obtain a Poisson limit theorem, as $n \to \infty$, for the number of large probability kth-nearest neighbor balls of $X_1,\ldots, X_n$. Our result generalizes Theorem 2.2 of [11], which refers to the special case $k=1$. Our proof is completely different since it employs the Chen–Stein method instead of the method of moments. Moreover, we obtain a rate of convergence for the Poisson approximation.

Coupons are collected one at a time from a population containing n distinct types of coupon. The process is repeated until all n coupons have been collected and the total number of draws, Y, from the population is recorded. It is assumed that the draws from the population are independent and identically distributed (draws with replacement) according to a probability distribution X with the probability that a type-i coupon is drawn being P(X = i). The special case where each type of coupon is equally likely to be drawn from the population is the classic coupon collector problem. We consider the asymptotic distribution Y (appropriately normalized) as the number of coupons n → ∞ under general assumptions upon the asymptotic distribution of X. The results are proved by studying the total number of coupons, W(t), not collected in t draws from the population and noting that P(Y ≤ t) = P(W(t) = 0). Two normalizations of Y are considered, the choice of normalization depending upon whether or not a suitable Poisson limit exists for W(t). Finally, extensions to the K-coupon collector problem and the birthday problem are given.

Consider a ·/G/k finite-buffer queue with a stationary ergodic arrival process and delayed customer feedback, where customers after service may repeatedly return to the back of the queue after an independent general feedback delay whose distribution has a continuous density function. We use coupling methods to show that, under some mild conditions, the feedback flow of customers returning to the back of the queue converges to a Poisson process as the feedback delay distribution is scaled up. This allows for easy waiting-time approximations in the setting of Poisson arrivals, and also gives a new coupling proof of a classic highway traffic result of Breiman (1963). We also consider the case of nonindependent feedback delays.

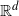
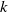
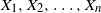
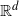
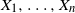
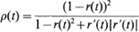
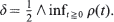Let ξ (t); t ≧ 0 be a normalized continuous mean square differentiable stationary normal process with covariance function r(t). Further, let and set . We give bounds which are roughly of order Τ –δ for the rate of convergence of the distribution of the maximum and of the number of upcrossings of a high level by ξ (t) in the interval [0, T]. The results assume that r(t) and r′(t) decay polynomially at infinity and that r ″ (t) is suitably bounded. For the number of upcrossings it is in addition assumed that r(t) is non-negative.

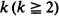In the present paper we study the number of occurrences of non-overlapping success runs of length in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.