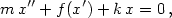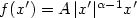Refine search
Actions for selected content:
4 results
Introduction
-
- Book:
- Attractors of Hamiltonian Nonlinear Partial Differential Equations
- Published online:
- 17 September 2021
- Print publication:
- 30 September 2021, pp 1-12
-
- Chapter
- Export citation
3 - Global Attraction to Stationary Orbits
-
- Book:
- Attractors of Hamiltonian Nonlinear Partial Differential Equations
- Published online:
- 17 September 2021
- Print publication:
- 30 September 2021, pp 91-113
-
- Chapter
- Export citation
Closed-Form Expression for the Exact Period of a Nonlinear Oscillator Typified by a Mass Attached to a Stretched Wire
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 3 / Issue 6 / December 2011
- Published online by Cambridge University Press:
- 03 June 2015, pp. 689-701
- Print publication:
- December 2011
-
- Article
- Export citation
The Nonlinearly Damped Oscillator
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 231-246
- Print publication:
- January 2003
-
- Article
- Export citation