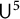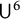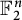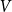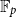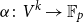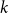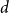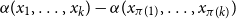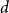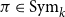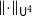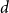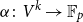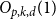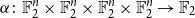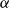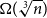Let 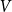 $V$ be a finite-dimensional vector space over
$V$ be a finite-dimensional vector space over 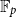 $\mathbb{F}_p$. We say that a multilinear form
$\mathbb{F}_p$. We say that a multilinear form 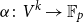 $\alpha \colon V^k \to \mathbb{F}_p$ in
$\alpha \colon V^k \to \mathbb{F}_p$ in 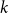 $k$ variables is
$k$ variables is 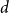 $d$-approximately symmetric if the partition rank of difference
$d$-approximately symmetric if the partition rank of difference 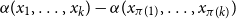 $\alpha (x_1, \ldots, x_k) - \alpha (x_{\pi (1)}, \ldots, x_{\pi (k)})$ is at most
$\alpha (x_1, \ldots, x_k) - \alpha (x_{\pi (1)}, \ldots, x_{\pi (k)})$ is at most 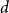 $d$ for every permutation
$d$ for every permutation 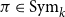 $\pi \in \textrm{Sym}_k$. In a work concerning the inverse theorem for the Gowers uniformity
$\pi \in \textrm{Sym}_k$. In a work concerning the inverse theorem for the Gowers uniformity 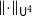 $\|\!\cdot\! \|_{\mathsf{U}^4}$ norm in the case of low characteristic, Tidor conjectured that any
$\|\!\cdot\! \|_{\mathsf{U}^4}$ norm in the case of low characteristic, Tidor conjectured that any 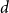 $d$-approximately symmetric multilinear form
$d$-approximately symmetric multilinear form 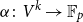 $\alpha \colon V^k \to \mathbb{F}_p$ differs from a symmetric multilinear form by a multilinear form of partition rank at most
$\alpha \colon V^k \to \mathbb{F}_p$ differs from a symmetric multilinear form by a multilinear form of partition rank at most 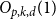 $O_{p,k,d}(1)$ and proved this conjecture in the case of trilinear forms. In this paper, somewhat surprisingly, we show that this conjecture is false. In fact, we show that approximately symmetric forms can be quite far from the symmetric ones, by constructing a multilinear form
$O_{p,k,d}(1)$ and proved this conjecture in the case of trilinear forms. In this paper, somewhat surprisingly, we show that this conjecture is false. In fact, we show that approximately symmetric forms can be quite far from the symmetric ones, by constructing a multilinear form 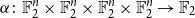 $\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$ which is 3-approximately symmetric, while the difference between
$\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$ which is 3-approximately symmetric, while the difference between 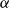 $\alpha$ and any symmetric multilinear form is of partition rank at least
$\alpha$ and any symmetric multilinear form is of partition rank at least 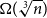 $\Omega (\sqrt [3]{n})$.
$\Omega (\sqrt [3]{n})$.
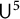 $\mathsf {U}^5$ and
$\mathsf {U}^5$ and 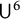 $\mathsf {U}^6$ in
$\mathsf {U}^6$ in 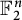 $\mathbb {F}_2^n$
$\mathbb {F}_2^n$