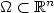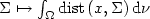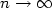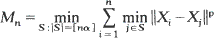Refine search
Actions for selected content:
3 results
Approximation by finitely supported measures
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 April 2011, pp. 343-359
- Print publication:
- April 2012
-
- Article
- Export citation
Long-term planning versus short-term planning in the asymptotical location problem
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 15 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 30 May 2008, pp. 509-524
- Print publication:
- July 2009
-
- Article
- Export citation
Steinhaus's geometric location problem for random samples in the plane
-
- Journal:
- Advances in Applied Probability / Volume 14 / Issue 1 / March 1982
- Published online by Cambridge University Press:
- 01 July 2016, pp. 56-67
- Print publication:
- March 1982
-
- Article
- Export citation