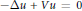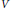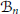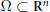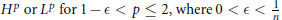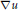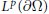Refine search
Actions for selected content:
2 results
Regularity of Standing Waves on Lipschitz Domains
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 3 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 702-720
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
On the Neumann Problem for the Schrödinger Equations with Singular Potentials in Lipschitz Domains
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 3 / 01 June 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 655-672
- Print publication:
- 01 June 2004
-
- Article
-
- You have access
- Export citation
-
We consider the Neumann problem for the Schrödinger equations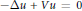
$-\Delta u\,+\,Vu\,=\,0$ , with singular nonnegative potentials 
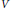$V$ belonging to the reverse Hölder class 
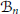${{\mathcal{B}}_{n}}$ , in a connected Lipschitz domain 
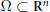$\Omega \,\subset \,{{\text{R}}^{n}}$ . Given boundary data 
$g$ in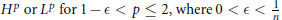 
${{H}^{p}}\text{or}\,{{L}^{p}}\,\text{for}\,\text{1}-\in \,<\,p\,\le \,2,\text{where}\,\text{0}<\in <\frac{1}{n}$ , it is shown that there is a unique solution, 
$u$ , that solves the Neumann problem for the given data and such that the nontangential maximal function of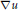 
$\nabla u$ is in 
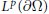${{L}^{p}}(\partial \Omega )$ . Moreover, the uniform estimates are found.
