Refine search
Actions for selected content:
1 results
FACTORIZATION OF OPERATORS THROUGH SUBSPACES OF
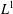$L^{1}$ -SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 313-328
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
-
We analyze domination properties and factorization of operators in Banach spaces through subspaces of
$L^{1}$ -spaces. Using vector measure integration and extending classical arguments based on scalar integral bounds, we provide characterizations of operators factoring through subspaces of 
$L^{1}$ -spaces of finite measures. Some special cases involving positivity and compactness of the operators are considered.
