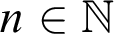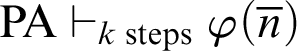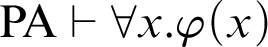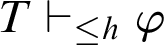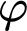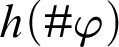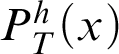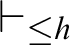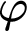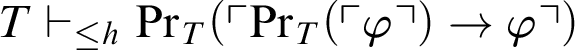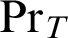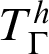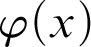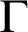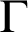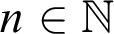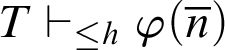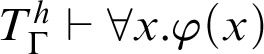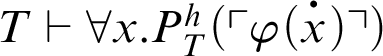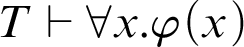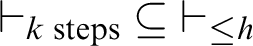Kreisel’s conjecture is the statement: if, for all 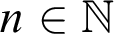$n\in \mathbb {N}$, 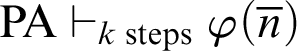$\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi (\overline {n})$, then 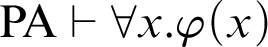$\mathop {\text {PA}} \nolimits \vdash \forall x.\varphi (x)$. For a theory of arithmetic T, given a recursive function h, 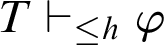$T \vdash _{\leq h} \varphi $ holds if there is a proof of 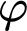$\varphi $ in T whose code is at most 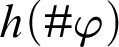$h(\#\varphi )$. This notion depends on the underlying coding. 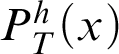${P}^h_T(x)$ is a predicate for 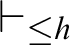$\vdash _{\leq h}$ in T. It is shown that there exist a sentence 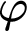$\varphi $ and a total recursive function h such that 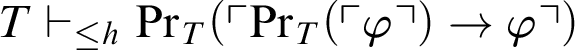$T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$, but 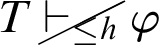, where 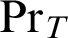$\mathop {\text {Pr}} \nolimits _T$ stands for the standard provability predicate in T. This statement is related to a conjecture by Montagna. Also variants and weakenings of Kreisel’s conjecture are studied. By the use of reflexion principles, one can obtain a theory 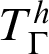$T^h_\Gamma $ that extends T such that a version of Kreisel’s conjecture holds: given a recursive function h and 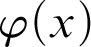$\varphi (x)$ a 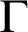$\Gamma $-formula (where 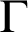$\Gamma $ is an arbitrarily fixed class of formulas) such that, for all 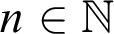$n\in \mathbb {N}$, 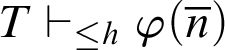$T\vdash _{\leq h} \varphi (\overline {n})$, then 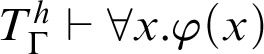$T^h_\Gamma \vdash \forall x.\varphi (x)$. Derivability conditions are studied for a theory to satisfy the following implication: if 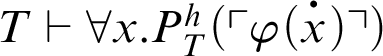, then 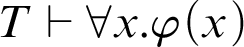$T\vdash \forall x.\varphi (x)$. This corresponds to an arithmetization of Kreisel’s conjecture. It is shown that, for certain theories, there exists a function h such that 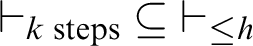$\vdash _{k \text { steps}}\ \subseteq\ \vdash _{\leq h}$.