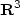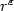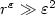Refine search
Actions for selected content:
3 results
A Hamilton-Jacobi approach to junction problems and application to traffic flows∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 March 2012, pp. 129-166
- Print publication:
- January 2013
-
- Article
- Export citation
Junction of elastic plates and beams
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 3 / July 2007
- Published online by Cambridge University Press:
- 26 July 2007, pp. 419-457
- Print publication:
- July 2007
-
- Article
- Export citation