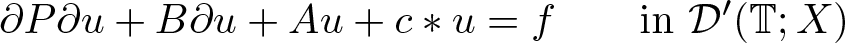Refine search
Actions for selected content:
10 results
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
MEASURES OF NONCOMPACTNESS IN A SOBOLEV SPACE AND INTEGRO-DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 497-506
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Analysis of a heterogeneous model for riot dynamics: the effect of censorship of information
-
- Journal:
- European Journal of Applied Mathematics / Volume 27 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 15 July 2015, pp. 554-582
-
- Article
- Export citation
Modelling Effects of Rapid Evolution on Persistence andStability in Structured Predator-Prey Systems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 3 / 2014
- Published online by Cambridge University Press:
- 28 May 2014, pp. 26-46
- Print publication:
- 2014
-
- Article
- Export citation
Populational adaptive evolution, chemotherapeutic resistanceand multiple anti-cancer therapies
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 2 / March 2013
- Published online by Cambridge University Press:
- 11 January 2013, pp. 377-399
- Print publication:
- March 2013
-
- Article
- Export citation
Pattern and Waves for a Model in Population Dynamics with Nonlocal Consumption ofResources
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 1 / Issue 1 / 2006
- Published online by Cambridge University Press:
- 15 May 2008, pp. 63-80
- Print publication:
- 2006
-
- Article
- Export citation
Ruin Probabilities for Two Classes of Risk Processes
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 35 / Issue 1 / May 2005
- Published online by Cambridge University Press:
- 17 April 2015, pp. 61-77
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
L∞(L2) and L∞(L∞) error estimates for mixed methodsfor integro-differential equations of parabolic type
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 33 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 531-546
- Print publication:
- May 1999
-
- Article
- Export citation
Stationary distributions under mutation-selection balance: structure and properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 227-251
- Print publication:
- March 1996
-
- Article
- Export citation