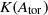Refine search
Actions for selected content:
3 results
Abelian varieties and Galois extensions of Hilbertian fields
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 16 May 2012, pp. 237-247
- Print publication:
- April 2013
-
- Article
- Export citation
Hilbertianity of fields of power series
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 351-361
- Print publication:
- April 2012
-
- Article
- Export citation
Diamonds in Torsion of Abelian Varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 10 February 2010, pp. 477-480
- Print publication:
- July 2010
-
- Article
- Export citation