We analyze the hereditarily ordinal definable sets $\operatorname {HOD} $ in $M_n(x)[g]$ for a Turing cone of reals x, where $M_n(x)$ is the canonical inner model with n Woodin cardinals build over x and g is generic over $M_n(x)$ for the Lévy collapse up to its bottom inaccessible cardinal. We prove that assuming $\boldsymbol \Pi ^1_{n+2}$-determinacy, for a Turing cone of reals x, $\operatorname {HOD} ^{M_n(x)[g]} = M_n(\mathcal {M}_{\infty } | \kappa _{\infty }, \Lambda ),$ where $\mathcal {M}_{\infty }$ is a direct limit of iterates of $M_{n+1}$, $\delta _{\infty }$ is the least Woodin cardinal in $\mathcal {M}_{\infty }$, $\kappa _{\infty }$ is the least inaccessible cardinal in $\mathcal {M}_{\infty }$ above $\delta _{\infty }$, and $\Lambda $ is a partial iteration strategy for $\mathcal {M}_{\infty }$. It will also be shown that under the same hypothesis $\operatorname {HOD}^{M_n(x)[g]} $ satisfies $\operatorname {GCH} $.

The HOD Dichotomy Theorem states that if there is an extendible cardinal, δ, then either HOD is “close” to V (in the sense that it correctly computes successors of singular cardinals greater than δ) or HOD is “far” from V (in the sense that all regular cardinals greater than or equal to δ are measurable in HOD). The question is whether the future will lead to the first or the second side of the dichotomy. Is HOD “close” to V, or “far” from V? There is a program aimed at establishing the first alternative—the “close” side of the HOD Dichotomy. This is the program of inner model theory. In recent years the third author has provided evidence that there is an ultimate inner model—Ultimate-L—and he has isolated a natural conjecture associated with the model—the Ultimate-L Conjecture. This conjecture implies that (assuming the existence of an extendible cardinal) that the first alternative holds—HOD is “close” to V. This is the future in which pattern prevails. In this paper we introduce a very different program, one aimed at establishing the second alternative—the “far” side of the HOD Dichotomy. This is the program of large cardinals beyond choice. Kunen famously showed that if AC holds then there cannot be a Reinhardt cardinal. It has remained open whether Reinhardt cardinals are consistent in ZF alone. It turns out that there is an entire hierarchy of choiceless large cardinals of which Reinhardt cardinals are only the beginning, and, surprisingly, this hierarchy appears to be highly ordered and amenable to systematic investigation, as we shall show in this paper. The point is that if these choiceless large cardinals are consistent then the Ultimate-L Conjecture must fail. This is the future where chaos prevails.

Supercompact extender based forcings are used to construct models with HOD cardinal structure different from those of V. In particular, a model where all regular uncountable cardinals are measurable in HOD is constructed.

Starting from large cardinals we construct a model of ZFC in which the GCH fails everywhere, but such that GCH holds in its HOD. The result answers a question of Sy Friedman. Also, relative to the existence of large cardinals, we produce a model of ZFC + GCH such that GCH fails everywhere in its HOD.

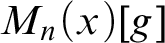
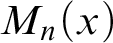
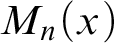
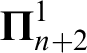
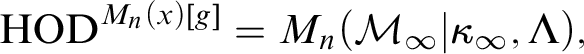
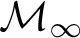
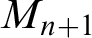
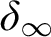
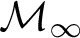
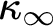
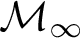
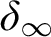
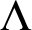
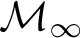
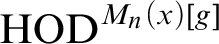
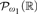In this paper, we explore the structure theory of L(ℝ, μ) under the hypothesis L(ℝ, μ) ⊧ “AD + μ is a normal fine measure on ” and give some applications. First we show that “ ZFC + there exist 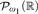ω2 Woodin cardinals”1 has the same consistency strength as “ AD + ω1 is ℝ-supercompact”. During this process we show that if L(ℝ, μ) ⊧ AD then in fact L(ℝ, μ) ⊧ AD+. Next we prove important properties of L(ℝ, μ) including Σ1 -reflection and the uniqueness of μ in L(ℝ, μ). Then we give the computation of full HOD in L(ℝ, μ). Finally, we use Σ1 -reflection and ℙmax forcing to construct a certain ideal on (or equivalently on 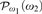in this situation) that has the same consistency strength as “ZFC+ there exist ω2 Woodin cardinals.”

This paper deals with the question whether the assumption that for every inaccessible cardinal κ there is a well-order of H(κ+) definable over the structure $\langle {\rm{H}}({\kappa ^ + }), \in \rangle$ by a formula without parameters is consistent with the existence of (large) large cardinals and failures of the GCH. We work under the assumption that the SCH holds at every singular fixed point of the ℶ-function and construct a class forcing that adds such a well-order at every inaccessible cardinal and preserves ZFC, all cofinalities, the continuum function, and all supercompact cardinals. Even in the absence of a proper class of inaccessible cardinals, this forcing produces a model of “V = HOD” and can therefore be used to force this axiom while preserving large cardinals and failures of the GCH. As another application, we show that we can start with a model containing an ω-superstrong cardinal κ and use this forcing to build a model in which κ is still ω-superstrong, the GCH fails at κ and there is a well-order of H(κ+) that is definable over H(κ+) without parameters. Finally, we can apply the forcing to answer a question about the definable failure of the GCH at a measurable cardinal.

Assume ZF + AD + V = L(ℝ) and let κ < Θ be an uncountable cardinal. We show that κ is Jónsson, and that if cof (κ) = ω then κ is Rowbottom. We also establish some other partition properties.