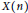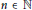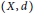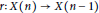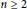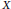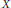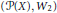Refine search
Actions for selected content:
13 results
Homogenisation of Wasserstein gradient flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 29 July 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractional time differential equations as a singular limit of the Kobayashi–Warren–Carter system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2024, pp. 1-37
-
- Article
- Export citation
From NeurODEs to AutoencODEs: A mean-field control framework for width-varying neural networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 February 2024, pp. 188-230
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the existence of a nodal solution for p-Laplacian equations depending on the gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 31 January 2024, pp. 1492-1513
- Print publication:
- August 2025
-
- Article
- Export citation
Minimizing movements for oscillating energies: the critical regime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 719-737
- Print publication:
- June 2019
-
- Article
- Export citation
Lipschitz Retractions in Hadamard Spaces via Gradient Flow Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-681
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
A Finite-Volume Method for Nonlinear Nonlocal Equations with a Gradient Flow Structure
-
- Journal:
- Communications in Computational Physics / Volume 17 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 November 2014, pp. 233-258
- Print publication:
- January 2015
-
- Article
- Export citation
Convergence of a variational Lagrangian scheme for a nonlineardrift diffusion equation∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 07 February 2014, pp. 697-726
- Print publication:
- May 2014
-
- Article
- Export citation
First Variation Formula in Wasserstein Spaces over Compact Alexandrov Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-735
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
First variation of the generalcurvature-dependent surface energy
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 59-79
- Print publication:
- January 2012
-
- Article
- Export citation
Weighted energy-dissipation functionals for gradient flows
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 30 October 2009, pp. 52-85
- Print publication:
- January 2011
-
- Article
- Export citation
Analysis of gradient flow of a regularized Mumford-Shahfunctional for image segmentation and image inpainting
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 291-320
- Print publication:
- March 2004
-
- Article
- Export citation
Analysis of total variation flow and its finite element approximations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 15 April 2004, pp. 533-556
- Print publication:
- May 2003
-
- Article
- Export citation