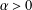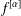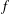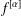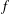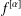Refine search
Actions for selected content:
10 results
ANALYSIS OF FOURTH-ORDER DIFFERENCE APPROXIMATION SCHEMES FOR FRACTIONAL DIFFUSION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 15 December 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractional Fick’s law and uphill transport of energetic particles at collisionless shocks
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 17 October 2025, E143
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integrable fractional Burgers hierarchy
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 31 July 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

High-Accuracy Finite Difference Methods
-
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LIMITS OF FRACTIONAL DERIVATIVES AND COMPOSITIONS OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 28 September 2016, pp. 104-115
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Fourth Order Difference Approximations for Space Riemann-Liouville Derivatives Based on Weighted and Shifted Lubich Difference Operators
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 2 / August 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 516-540
- Print publication:
- August 2014
-
- Article
- Export citation
Local Discontinuous Galerkin methods for fractional diffusionequations∗∗∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1845-1864
- Print publication:
- November 2013
-
- Article
- Export citation
THE FUNDAMENTAL AND NUMERICAL SOLUTIONS OF THE RIESZ SPACE-FRACTIONAL REACTION–DISPERSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 45-57
-
- Article
-
- You have access
- Export citation
Remarks on the relation between fractional moments and fractional derivatives of characteristic functions
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 456-466
- Print publication:
- June 1980
-
- Article
- Export citation