Refine search
Actions for selected content:
9 results
A CRITERION FOR ENSURING POSITIVITY OF FOURIER TRANSFORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 August 2025, pp. 1-11
-
- Article
- Export citation
10 - Fourier Analysis
- from Part II - Mathematical Methods
-
- Book:
- An Introduction to Continuum Physics
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 519-569
-
- Chapter
- Export citation
Measuring multidimensional heterogeneity in emergent social phenomena
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 316-327
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Fourier Transforms
-
- Book:
- The Observation and Analysis of Stellar Photospheres
- Published online:
- 05 January 2022
- Print publication:
- 16 December 2021, pp 27-49
-
- Chapter
- Export citation
6 - Data Transformations
-
- Book:
- Seismic Wave Theory
- Published online:
- 15 March 2019
- Print publication:
- 28 March 2019, pp 230-241
-
- Chapter
- Export citation
1 - Vectors, Tensors, and Fourier Transforms
-
- Book:
- Seismic Wave Theory
- Published online:
- 15 March 2019
- Print publication:
- 28 March 2019, pp 1-50
-
- Chapter
- Export citation
On the support of tempered distributions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 255-270
-
- Article
-
- You have access
- Export citation
Detailed probabilistic analysis of the integrated three-valued telegraph signal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 671-684
- Print publication:
- September 1997
-
- Article
- Export citation
On generalized functions
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue A / 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-156
- Print publication:
- 1982
-
- Article
- Export citation









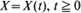 is examined. In particular, the third-order equations governing the distributions
is examined. In particular, the third-order equations governing the distributions 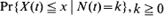 , (where
, (where 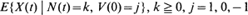 (where
(where 