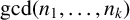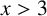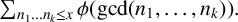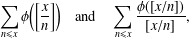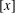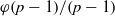Refine search
Actions for selected content:
4 results
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
- Export citation
NOTE ON SUMS INVOLVING THE EULER FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 194-200
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DISTRIBUTION FUNCTION OF
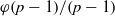 $ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
$ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 16 January 2013, pp. 77-83
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation