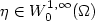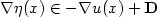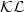Refine search
Actions for selected content:
11 results
Generic ill-posedness of the energy–momentum equations and differential inclusions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 26 September 2023, pp. 470-495
- Print publication:
- April 2025
-
- Article
- Export citation
Fixed points of multivalued maps under local Lipschitz conditions and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1467-1494
- Print publication:
- June 2020
-
- Article
- Export citation
Zeno breaking, the Contact effect and sensitive behaviour in piecewise-linear systems
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 826-844
-
- Article
-
- You have access
- Export citation
Convergence of a Time Discretization for a Nonlinear Second-Order Inclusion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 29 May 2017, pp. 93-120
-
- Article
- Export citation
Three periodic solutions for discontinuous perturbations of the vector p-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 673-681
- Print publication:
- August 2017
-
- Article
- Export citation
BV solutions and viscosity approximations of rate-independentsystems∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 23 December 2010, pp. 36-80
- Print publication:
- January 2012
-
- Article
- Export citation
Generalized solutions to hybrid dynamical systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 14 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 February 2008, pp. 699-724
- Print publication:
- October 2008
-
- Article
- Export citation
ON THE METHOD OF APPROXIMATION FOR EVOLUTIONARY INCLUSIONS OF PSEUDOMONOTONE TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 115-143
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
On the existence of variations, possibly with pointwise gradient constraints
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 12 May 2007, pp. 331-342
- Print publication:
- April 2007
-
- Article
- Export citation
Numerical precision for differential inclusionswith uniqueness
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 427-460
- Print publication:
- May 2002
-
- Article
- Export citation
A smooth Lyapunov function from a class- ${\mathcal{KL}}$
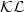 estimateinvolving two positive semidefinite functions
estimateinvolving two positive semidefinite functions
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 5 / 2000
- Published online by Cambridge University Press:
- 15 August 2002, pp. 313-367
- Print publication:
- 2000
-
- Article
- Export citation
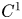
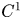
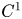
 .
.