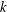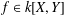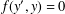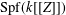Refine search
Actions for selected content:
4 results
Infinite matroids in tropical differential algebra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFORMATIONS OF DIFFERENTIAL ARCS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 405-410
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
A Differential Algebraic Method for the Solution of the Poisson Equation for Charged Particle Beams
-
- Journal:
- Communications in Computational Physics / Volume 17 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 November 2014, pp. 47-78
- Print publication:
- January 2015
-
- Article
- Export citation
On subgroups of the additive group in differentially closed fields
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 369-391
- Print publication:
- June 2012
-
- Article
- Export citation





 . If
. If