Refine search
Actions for selected content:
1 results
Opposing average congruence class biases in the cyclicity and Koblitz conjectures for elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The cyclicity and Koblitz conjectures ask about the distribution of primes of cyclic and prime-order reduction, respectively, for elliptic curves over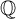
$\mathbb {Q}$. In 1976, Serre gave a conditional proof of the cyclicity conjecture, but the Koblitz conjecture (refined by Zywina in 2011) remains open. The conjectures are now known unconditionally “on average” due to work of Banks–Shparlinski and Balog–Cojocaru–David. Recently, there has been a growing interest in the cyclicity conjecture for primes in arithmetic progressions (AP), with relevant work by Akbal–Güloğlu and Wong. In this article, we adapt Zywina’s method to formulate the Koblitz conjecture for AP and refine a theorem of Jones to establish results on the moments of the constants in both the cyclicity and Koblitz conjectures for AP. In doing so, we uncover a somewhat counterintuitive phenomenon: On average, these two constants are oppositely biased over congruence classes. Finally, in an accompanying repository, we give Magma code for computing the constants discussed in this article.
