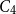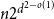Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

4 results

  • Crus and Lex in the Apse Mosaic of San Clemente

  • Margaret Atkins
  • Journal:
    New Blackfriars / Volume 106 / Issue 3 / May 2025
    Published online by Cambridge University Press:
    11 April 2025, pp. 203-207
    Print publication:
    May 2025
    • Article
      • You have access
      • Open access
    • PDF
    • HTML
    • Export citation

  • The famous apse mosaic of San Clemente in Rome has been thoroughly studied, but it is so rich that it still has the capacity to surprise. This article focuses on the inscription below the apse and points out that one word is standardly misread: the word is not CRUX (‘Cross’), but CRUS. This turns out to have a highly relevant sense. The article explores the implications of this word and of the inscription more widely.1

  • Many Hamiltonian subsets in large graphs with given density

  • Part of
  • Stijn Cambie, Jun Gao, Hong Liu
  • Journal:
    Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
    Published online by Cambridge University Press:
    02 October 2023, pp. 110-120

  • A set of vertices in a graph is a Hamiltonian subset if it induces a subgraph containing a Hamiltonian cycle. Kim, Liu, Sharifzadeh, and Staden proved that for large $d$, among all graphs with minimum degree $d$, $K_{d+1}$ minimises the number of Hamiltonian subsets. We prove a near optimal lower bound that takes also the order and the structure of a graph into account. For many natural graph classes, it provides a much better bound than the extremal one ($\approx 2^{d+1}$). Among others, our bound implies that an $n$-vertex $C_4$-free graph with minimum degree $d$ contains at least $n2^{d^{2-o(1)}}$ Hamiltonian subsets.