Refine search
Actions for selected content:
2 results
Constrained Approximation with Jacobi Weights
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-128
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
-
In this paper, we prove that for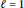
$\ell \,=\,1$ or 2 the rate of best 
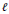$\ell $ - monotone polynomial approximation in the 
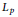${{L}_{p}}$ norm 
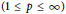$\left( 1\,\le \,p\,\le \,\infty\right)$ weighted by the Jacobi weight 
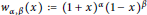${{w}_{\alpha ,\,\beta }}\left( x \right)\,:=\,{{\left( 1\,+\,x \right)}^{\alpha }}{{\left( 1\,-\,x \right)}^{\beta }}$ with 
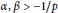$\alpha ,\,\beta \,>\,-1/p$ if 
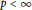$p\,<\,\infty $ , or 
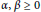$\alpha ,\,\beta \,\ge \,0$ if 
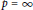$p\,=\,\infty $ , is bounded by an appropriate 
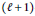$\left( \ell \,+\,1 \right)$ -st modulus of smoothness with the same weight, and that this rate cannot be bounded by the 
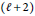$\left( \ell \,+\,2 \right)$ -nd modulus. Related results on constrained weighted spline approximation and applications of our estimates are also given.
Constrained Approximation in Sobolev Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 1 / 01 February 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-99
- Print publication:
- 01 February 1997
-
- Article
-
- You have access
- Export citation
-
Positive, copositive, onesided and intertwining (co-onesided) polynomial and spline approximations of functions
are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.
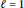
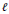
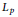
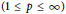
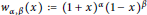
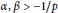
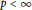
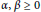
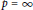
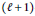
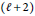
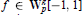are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.