Refine search
Actions for selected content:
13 results
1 - Introduction
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 1-6
-
- Chapter
-
- You have access
- Export citation

Modular Forms and String Theory
-
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024
COUPLED FREE FERMION CONFORMAL FIELD THEORY AND REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 April 2024, p. 170
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
5 - Two-Dimensional Conformal Field Theories
- from Part II - TheWorld-Sheet Perspective
-
- Book:
- A Short Introduction to String Theory
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 63-77
-
- Chapter
- Export citation
4 - The Free Massless Scalar Field on the Complex Plane
- from Part II - TheWorld-Sheet Perspective
-
- Book:
- A Short Introduction to String Theory
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 49-62
-
- Chapter
- Export citation
22 - Alexander Polyakov
-
- Book:
- Conversations on Quantum Gravity
- Published online:
- 05 August 2021
- Print publication:
- 26 August 2021, pp 428-439
-
- Chapter
- Export citation
12 - Spacetime and Physical Equivalence
- from Part III - Issues of Interpretation
-
-
- Book:
- Beyond Spacetime
- Published online:
- 24 April 2020
- Print publication:
- 14 May 2020, pp 257-283
-
- Chapter
- Export citation
17 - Riemann Tensor Correlator in de Sitter
- from Part V - Quantum Curvature Fluctuations in de Sitter Spacetime
-
- Book:
- Semiclassical and Stochastic Gravity
- Published online:
- 20 January 2020
- Print publication:
- 05 March 2020, pp 519-539
-
- Chapter
- Export citation
16 - Two-Point Metric Perturbations in de Sitter
- from Part V - Quantum Curvature Fluctuations in de Sitter Spacetime
-
- Book:
- Semiclassical and Stochastic Gravity
- Published online:
- 20 January 2020
- Print publication:
- 05 March 2020, pp 483-518
-
- Chapter
- Export citation
Higher-Level
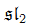 Conformal Blocks Divisors on
Conformal Blocks Divisors on 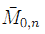
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 16 January 2014, pp. 7-30
-
- Article
-
- You have access
- Export citation
Modular Invariants and Twisted Equivariant K-theory II: Dynkin diagram symmetries
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 26 June 2013, pp. 273-330
- Print publication:
- October 2013
-
- Article
- Export citation
Correlation Functions and Boundary Conditions in Rational Conformal Field Theory and Three-Dimensional Topology
-
- Journal:
- Compositio Mathematica / Volume 131 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 189-238
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
The Level 2 and 3 Modular Invariants for the Orthogonal Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 3 / 01 June 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-521
- Print publication:
- 01 June 2000
-
- Article
-
- You have access
- Export citation
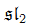 Conformal Blocks Divisors on
Conformal Blocks Divisors on 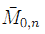
 modular invariant of SU(2), as well as some families of finite group doubles. This new
modular invariant of SU(2), as well as some families of finite group doubles. This new 













