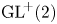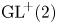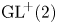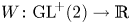Refine search
Actions for selected content:
31 results
7 - The Lagrangian Formalism
-
- Book:
- Classical Mechanics
- Published online:
- 26 June 2025
- Print publication:
- 19 June 2025, pp 154-209
-
- Chapter
- Export citation
Generic ill-posedness of the energy–momentum equations and differential inclusions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 26 September 2023, pp. 470-495
- Print publication:
- April 2025
-
- Article
- Export citation
7 - Variational Data Assimilation
- from Part III - Methods and Issues
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 163-209
-
- Chapter
- Export citation
A rank-one convex, nonpolyconvex isotropic function on
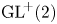 $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
$\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 February 2022, pp. 356-381
- Print publication:
- April 2022
-
- Article
- Export citation
8 - Euler and analysis: case studies and historiographical perspectives
-
-
- Book:
- Anachronisms in the History of Mathematics
- Published online:
- 19 July 2021
- Print publication:
- 22 July 2021, pp 223-250
-
- Chapter
- Export citation
WHY IS OPTIMAL GROWTH THEORY MUTE? RESTORING ITS RIGHTFUL VOICE
-
- Journal:
- Macroeconomic Dynamics / Volume 22 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 77-100
-
- Article
- Export citation
MATHEMATICAL MODELLING IN NANOTECHNOLOGY USING CALCULUS OF VARIATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 350-351
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Existence and conditional energetic stability of solitary gravity–capillary water waves with constant vorticity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 791-883
- Print publication:
- August 2015
-
- Article
- Export citation
Nonsmooth Problems of Calculus of Variationsvia Codifferentiation∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 08 August 2014, pp. 1153-1180
- Print publication:
- October 2014
-
- Article
- Export citation
Transport problems and disintegration maps
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 888-905
- Print publication:
- July 2013
-
- Article
- Export citation
GLOBAL SOLUTIONS OF THE EQUATION OF THE KIRCHHOFF ELASTIC ROD IN SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 27 September 2012, pp. 70-80
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
The extended adjoint method
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 July 2012, pp. 83-108
- Print publication:
- January 2013
-
- Article
- Export citation
Subriemannian geodesics of Carnot groups of step 3∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 274-287
- Print publication:
- January 2013
-
- Article
- Export citation
Mathematical Modeling of Large-Amplitude Dynamic-Plastic Behavior of Circular Plates Subjected to Impulsive Loads
-
- Journal:
- Journal of Mechanics / Volume 26 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 03 October 2011, pp. 533-546
- Print publication:
- December 2010
-
- Article
- Export citation
Scaling laws for non-Euclidean plates and theW2,2 isometric immersions of Riemannian metrics
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 1158-1173
- Print publication:
- October 2011
-
- Article
- Export citation
A note on convergence of low energy critical pointsof nonlinear elasticity functionals,for thin shells of arbitrary geometry
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 24 March 2010, pp. 493-505
- Print publication:
- April 2011
-
- Article
- Export citation
The problem of the body of revolutionof minimal resistance
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 19 December 2008, pp. 206-220
- Print publication:
- January 2010
-
- Article
- Export citation
An a priori Campanato type regularity condition for local minimisers in the calculus of variations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 21 October 2008, pp. 111-131
- Print publication:
- January 2010
-
- Article
- Export citation
Optimal partial regularity of minimizers of quasiconvex variational integrals
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 05 September 2007, pp. 639-656
- Print publication:
- October 2007
-
- Article
- Export citation
Optimal control problems on parallelizable Riemannian manifolds: theory and applications
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 15 December 2005, pp. 1-11
- Print publication:
- January 2006
-
- Article
- Export citation