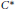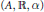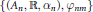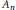Refine search
Actions for selected content:
2 results
Classification of Inductive Limits of Outer Actions of ℝ on Approximate Circle Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-80
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
-
In this paper we present a classification, up to equivariant isomorphism, of
${{C}^{*}}$ -dynamical systems 
$(A,\,\mathbb{R},\,\alpha )$ arising as inductive limits of directed systems 
$\{({{A}_{n}},\,\mathbb{R},\,{{\alpha }_{n}}),\,{{\varphi }_{nm}}\}$ , where each 
${{A}_{n}}$ is a finite direct sum of matrix algebras over the continuous functions on the unit circle, and the 
${{\alpha }_{n}}\text{s}$ are outer actions generated by rotation of the spectrum.
ON TENSOR PRODUCTS OF WEAK MIXING VECTOR SEQUENCES AND THEIR APPLICATIONS TO UNIQUELY E-WEAK MIXING C*-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 46-59
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
