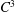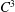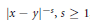Refine search
Actions for selected content:
10 results
High Order Energy-Preserving Method of the “Good” Boussinesq Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 15 February 2016, pp. 111-122
- Print publication:
- February 2016
-
- Article
- Export citation
Interior Penalty Discontinuous Galerkin Based Isogeometric Analysis for Allen-Cahn Equations on Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1380-1416
- Print publication:
- November 2015
-
- Article
- Export citation
Multi-Symplectic Method for the Zakharov-Kuznetsov Equation
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 58-73
- Print publication:
- February 2015
-
- Article
- Export citation
Interpolation by G2 Quintic Pythagorean-Hodograph Curves
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 374-398
- Print publication:
- August 2014
-
- Article
- Export citation
A symmetric
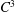 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 259-272
-
- Article
-
- You have access
- Export citation
Generalized and Unified Families of Interpolating Subdivision Schemes
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 193-213
- Print publication:
- May 2014
-
- Article
- Export citation
Numerical Method of Fabric Dynamics Using Front Tracking and Spring Model
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 5 / November 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1228-1251
- Print publication:
- November 2013
-
- Article
- Export citation
Stroke-Based Surface Reconstruction
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 297-324
- Print publication:
- February 2013
-
- Article
- Export citation
Lower Order Terms of the Discrete Minimal Riesz Energy on Smooth Closed Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 1 / 01 February 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-43
- Print publication:
- 01 February 2012
-
- Article
-
- You have access
- Export citation
Cubic Spiral Transition Matching G2 Hermite End Conditions
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 4 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 525-536
- Print publication:
- November 2011
-
- Article
- Export citation
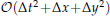 is proposed. The multi-symplectic conservation property of the new scheme is proved. The backward error analysis of the new multi-symplectic scheme is also implemented. The solitary wave evolution behaviors of the Zakharov-Kunetsov equation is investigated by the new multi-symplectic scheme. The accuracy of the scheme is analyzed.
is proposed. The multi-symplectic conservation property of the new scheme is proved. The backward error analysis of the new multi-symplectic scheme is also implemented. The solitary wave evolution behaviors of the Zakharov-Kunetsov equation is investigated by the new multi-symplectic scheme. The accuracy of the scheme is analyzed.