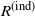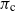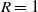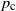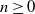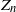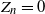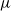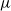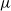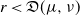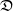Refine search
Actions for selected content:
372 results
Conditioning Bienaymé–Galton–Watson trees to have large sub-populations
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-42
-
- Article
- Export citation
Quasi-stationary distributions for subcritical branching Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-47
-
- Article
- Export citation
The distance on the slightly supercritical random series–parallel graph
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Negative moments of the CREM partition function in the high-temperature regime
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 29 July 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The replicator coalescent
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ergodic theorem for branching markov chains indexed by trees with arbitrary shape
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1089-1104
- Print publication:
- September 2025
-
- Article
- Export citation
Epidemic models with digital and manual contact tracing
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviors of subcritical branching killed Brownian motion with drift
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1-26
-
- Article
- Export citation
Some conditional properties of superprocesses in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1156-1172
- Print publication:
- September 2025
-
- Article
- Export citation
The real-time growth rate of stochastic epidemics on random intersection graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1132-1155
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The speed of a biased walk on a Galton–Watson tree without leaves is monotonic for low values of bias
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1044-1052
- Print publication:
- September 2025
-
- Article
-
- You have access
- HTML
- Export citation
Long edges in Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1053-1068
- Print publication:
- September 2025
-
- Article
- Export citation
The number of individuals alive in a branching process given only times of deaths
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. 871-906
- Print publication:
- September 2025
-
- Article
- Export citation
Convergence of the derivative martingale for the branching random walk in time-inhomogeneous random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 642-676
- Print publication:
- June 2025
-
- Article
- Export citation
Gaussian fluctuations for the two-urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 607-641
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
First-passage time for Sinai’s random walk in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 29 November 2024, pp. 756-774
- Print publication:
- June 2025
-
- Article
- Export citation
Regeneration of branching processes with immigration in varying environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 422-444
- Print publication:
- March 2025
-
- Article
- Export citation
On the strong stability of ergodic iterations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 284-297
- Print publication:
- March 2025
-
- Article
- Export citation
Stationary measures and the continuous-state branching process conditioned on extinction
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 07 October 2024, pp. 576-602
- Print publication:
- June 2025
-
- Article
- Export citation
Maximum likelihood estimation for spinal-structured trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 234-268
- Print publication:
- March 2025
-
- Article
- Export citation