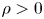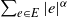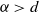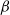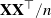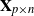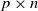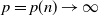Refine search
Actions for selected content:
207 results
Quasi-stationary distributions for subcritical branching Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-47
-
- Article
- Export citation
A large deviation principle for block models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-74
-
- Article
- Export citation
Infinite-horizon Fuk–Nagaev inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1076-1088
- Print publication:
- September 2025
-
- Article
- Export citation
Moderate deviations for weight-dependent random connection models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1-23
-
- Article
- Export citation
Sample path moderate deviations for non-stationary power-law shot noise processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1105-1131
- Print publication:
- September 2025
-
- Article
- Export citation
Large deviation principle for slow-fast rough differential equations via controlled rough paths
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-31
-
- Article
- Export citation
Measure comparison problems for dilations of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 270-285
- Print publication:
- March 2025
-
- Article
- Export citation
Moderate deviations of many-server queues via idempotent processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 708-742
- Print publication:
- June 2025
-
- Article
- Export citation
Gaussian approximation and moderate deviations of Poisson shot noises with application to compound generalized Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 305-345
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Precise large deviations of the net loss process in a non-standard two-dimensional risk model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 44-63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tail asymptotics and precise large deviations for some Poisson cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 26 July 2024, pp. 204-240
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sufficient condition for the quasipotential to be the rate function of the invariant measure of countable-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 960-1003
- Print publication:
- September 2024
-
- Article
- Export citation
Asymptotic results for sums and extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 1153-1171
- Print publication:
- December 2024
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
- Export citation
An exponential nonuniform Berry–Esseen bound of the maximum likelihood estimator in a Jacobi process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 909-926
- Print publication:
- September 2024
-
- Article
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation
Propagation of chaos and large deviations in mean-field models with jumps on block-structured networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1301-1361
- Print publication:
- December 2023
-
- Article
- Export citation
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation